模板
乱七八糟
语法
to_string//转换成字符串
stroll //转化成数字
//set用法
st.insert(x) //st中插入一个元素x
st.size() //返回集合set中元素的个数
st.begin() //set集合起始地址
st.end() //set集合结束的地址
set<Type>::iterator it; //定义一个对应类型的迭代器 来遍历set
set遍历:for(auto it = set.begin();auto != set.end(),it++)
set.find(x)找不到就返回st.end();
//map用法
map<char, int> q;
q.insert(pair<int, string>(111, "kk"));
遍历map
for(pair<char,int> x:q)
{
cout<<x.first<<' '<<x.second<<'\n';
}
substr(0,i)输出(0,i)的子串
lambda表达式
auto dfs = [&](auto dfs,int g,int step) -> void{ 第一个参数代表递归
if(step == len){ //搜到了这么多因子了
if(check(g) && g > n - k){
++ans;
}
return;
}
int t = 1;
for(int c = 0;c <= zhi[step];c++){ //筛法
if(c) t*=di[step];
dfs(dfs,g*t,step + 1);
}
};
dfs(dfs, 1, 0);求一个数二进制1的个数
void count(int m){
int tmp = 0;
while(m > 0){
tmp++;
m &= (m - 1);
}
}当后缀和不好维护的时候,考虑后缀和等于总和减去前缀和,转换成总和减前缀和
处理向上取整
快读快写
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9')
x=x*10+ch-'0',ch=getchar();
return x*f;
}
void write(int x)
{
if(x<0)
putchar('-'),x=-x;
if(x>9)
write(x/10);
putchar(x%10+'0');
return;
}二分
最大化查找(查找第一个<=q的数的下标)
#include <bits/stdc++.h>
using namespace std;
int find(int q){
int l = 0,r = n + 1;
while(l + 1 < r){
int mid =l + (r - l) / 2;
if(a[mid] <= q) l = mid;
else r= mid;
}
return l;
}
lowerbound(begin,end,value) //求的是第一个大于等于
upperbound(begin,end,value) //求的是第一个大于最小化查找(查找第一个>=q的数的下标)
int find(int q){
int l = 0,r = n + 1;
while(l + 1 < r){
int mid =l + (r - l) / 2;
if(a[mid] >= q) r = mid;
else l= mid;
}
return r;
}二分答案
bool check(){
}//用来判断答案是否可行
int l = 1,r = MAXN,mid = (l + r) >> 1;
int c;
while(l <= r){ //二分查找
c = check(mid);
if(c){
r = mid - 1;
mid = (l + r) >> 1;
}else{
l = mid + 1;
mid = (l + r) >> 1;
}
}数学
位运算
消去x最后一位的1
x&(x-1)比如: 十进制数10的二进制为1010,9的二进制数为1001,那么(1010)&(1001)=1000,现在10的二进制中最后一位的1已经被消去
用途:
可以用来检测一个数是不是2的幂次。
如果一个数
x是2的幂次,那么x>0且x的二进制中只有一个1,所以用x&(x-1)把1消去,应该返回0,如果返回了非0值,证明不是2的幂次计算一个整数二进制中1的个数
因为1可以不断的通过
x&(x-1)这个操作消去,所以当最后的值变成0的时候,也就求出了二进制中1的个数如果将整数
A转换成整数B,需要改变多少个比特位.思考将整数A转换为B,如果A和B在第i(0<=i<32)个位上相等,则不需要改变这个BIT位,如果在第i位上不相等,则需要改变这个BIT位。所以问题转化为了A和B有多少个BIT位不相同。联想到位运算有一个异或操作,相同为0,相异为1,所以问题转变成了计算A异或B之后这个数中1的个数
其他常用操作:
| 功能 | 示例 | 位运算 |
|---|---|---|
| 去掉最后一位 | (101101->10110) | x shr 1 |
| 在最后加一个0 | (101101->1011010) | x shl 1 |
| 在最后加一个1 | (101101->1011011) | x shl 1+1 |
| 把最后一位变成1 | (101100->101101) | x or 1 |
| 把最后一位变成0 | (101101->101100) | x or 1-1 |
| 最后一位取反 | (101101->101100) | x xor 1 |
| 把右数第k位变成1 | (101001->101101,k=3) | x or (1 shl (k-1)) |
| 把右数第k位变成0 | (101101->101001,k=3) | x and not (1 shl (k-1)) |
| 右数第k位取反 | (101001->101101,k=3) | x xor (1 shl (k-1)) |
| 取末三位 | (1101101->101) | x and 7 |
| 取末k位 | (1101101->1101,k=5) | x and (1 shl k-1) |
| 取右数第k位 | (1101101->1,k=4) | x shr (k-1) and 1 |
| 把末k位变成1 | (101001->101111,k=4) | x or (1 shl k-1) |
| 末k位取反 | (101001->100110,k=4) | x xor (1 shl k-1) |
| 把右边连续的1变成0 | (100101111->100100000) | x and (x+1) |
| 把右起第一个0变成1 | (100101111->100111111) | x or (x+1) |
| 把右边连续的0变成1 | (11011000->11011111) | x or (x-1) |
| 取右边连续的1 | (100101111->1111) | (x xor (x+1)) shr 1 |
| 去掉右起第一个1的左边 | (100101000->1000) | x and (x xor (x-1)) |
利用二进制来枚举子集
假设我们现在有5个小球,上面分别标号了0,1,2,3,4代表这些小球的权值,现在要像你求出这些小球的权值可以组成的所有情况。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n=5;//5个小球
for(int i=0; i<(1<<n); i++) //从0~2^5-1个状态
{
for(int j=0; j<n; j++) //遍历二进制的每一位
{
if(i&(1<<j))//判断二进制第j位是否存在
{
printf("%d ",j);//如果存在输出第j个元素
}
}
printf("\n");
}
return 0;
}异或操作
异或的性质:
x^x=0;
x^0=x;用途:
数组中,只有一个数出现一次,剩下都出现两次,找出出现一次的数
因为剩下的都出现了两次,那么异或值肯定为0,所以把所有的数异或起来得到的值就是那个数,可以做一下
nyoj-528找球号(三)个没有游标的天平,和n个秤砣,m个询问, 每次一个k,问可否秤出k这个重量。秤砣可以放两边。
bitset保存状态,用移位操作来转移。
#include <bits/stdc++.h> using namespace std; const int offset = 2005; int w[22]; int main() { int T; scanf("%d", &T); while(T--) { int n; scanf("%d", &n); for(int i = 0; i < n; i++) scanf("%d", &w[i]); bitset <4005> f; f[offset] = 1; for(int i = 0; i < n; i++){ f = f | (f << w[i]) | (f >> w[i]); } int q, k; scanf("%d", &q); while(q--){ scanf("%d", &k); if(f[offset - k] || f[offset + k]) puts("YES"); else puts("NO"); } } return 0; }待补充。
行列式计算
int det(int a[N][N], int n) {
int res = 0;
if (n == 1) {
return a[0][0];
} else {
for (int j = 0; j < n; j++) {
int t[N][N];
for (int i = 1; i < n; i++) {
int k = 0;
for (int p = 0; p < n; p++) {
if (p == j) {
continue;
}
t[i - 1][k++] = a[i][p];
}
}
res += ((j % 2 == 1) ? -1 : 1) * a[0][j] * det(t, n - 1);
}
}
return res;
}欧拉筛
const int N=1e8;
int primes[N],cnt; // 存放质数
bool st[N]; // 当前数是否被筛
int minp[N]; // 保存最小质因子
int get_primes(int n) // 欧拉筛 O(n)
{
for(int i=2;i<=n;i++)
{
if(!st[i]) // 若i没被筛去 此时i必为质数
{
minp[i]=i; // i的最小的质因子为i
primes[cnt++]=i; // 将i保存在primes数组中 cnt往后移动一位
}
for(int j=0;i*primes[j]<=n;j++)
{
int t=primes[j]*i; // 得到质数的倍数
st[t] = true; // 质数的倍数被筛去
minp[t]=primes[j]; // 质数的倍数最小的质因子就是该质数
if(i%primes[j]==0) break;
// 若i是之前素数的倍数
// 说明这个倍数会在后面的循环内被筛去
// 没有必要继续循环了
}
}
}逆元
加法中元素的逆元为-a,在乘法运算中a的逆元为
逆元可以用乘法代替除法实现除法意义的取模运算

img
递推求逆元
int ans[N];
void pre(int n)
{
int ans[1]=1;
for(int i=2;i<=n;i++){
ans[i]=(mod-mod/i)*ans[mod%i]%mod;
}快速幂求逆元
a/b
ans = a*qpow(b,p - 2,p);鸽巢原理
如果要把n + 1个物体放进n个盒子,那么至少有一个盒子包含两个或更多的物体
加强版
设为正整数,如果将个物体放入n个盒子内,那么或者第一个盒子内至少含有个物体或者第二个盒子内至少含有个物体..........第n个盒子内至少含有个物体。
组合数
二项式定理
其中 =递推法
const int N = 2010, mod = 1e9 + 7;
int C[N][N];
void init(){
for(int i = 0; i < N; i++) C[i][0] = C[i][i] = 1;
for(int i = 1; i < N; i++)
for(int j = 1; j < i; j++)
C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
}快速幂
int ksm(int x,int y)
{
x%=mod;
int num=1;
while(y){
if(y&1)num=num*x%mod;
y>>=1;
x=x*x%mod;
}
return num;
}
int jie[N],nijie[N];
void pre(int n)
{
jie[0]=1;
for(int i=1;i<=n;i++){
jie[i]=jie[i-1]*i%mod;
}
nijie[n]=ksm(jie[n],mod-2);
for(int i=n;i>=1;i--){
nijie[i-1]=nijie[i]*i%mod;
}
}
int C(int n,int m)
{
if(m<0||n<m)return 0;
return jie[n]*nijie[m]%mod*nijie[n-m]%mod;
}欧拉函数
。 因为p是质数,所以~中间除了p的倍数之外所有数都与p互质,而p的倍数的个数是1.如果只求φ(n),唯一分解 那么我们就直接将n唯一分解处理出每一个n的素数,然后用通项公式就行了。 效率:O(√n)
#include <cmath>
int euler_phi(int n) {
int ans = n;
for (int i = 2; i * i <= n; i++)
if (n % i == 0) {
ans = ans / i * (i - 1);
while (n % i == 0) n /= i;
}
if (n > 1) ans = ans / n * (n - 1);
return ans;
}2.如果要求一个区域内的欧拉函数用唯一分解就太慢了,用到积性公式去做分解
vector<int> pri;
bool not_prime[N];
int phi[N];
void pre(int n) {
phi[1] = 1;
for (int i = 2; i <= n; i++) {
if (!not_prime[i]) {
pri.push_back(i);
phi[i] = i - 1;
}
for (int pri_j : pri) {
if (i * pri_j > n) break;
not_prime[i * pri_j] = true;
if (i % pri_j == 0) {
phi[i * pri_j] = phi[i] * pri_j;
break;
}
phi[i * pri_j] = phi[i] * phi[pri_j];
}
}
}欧拉定理
若正整数a,n互质,则有
如
莫比乌斯函数
反演结论
裴蜀定理
在数论中,裴蜀定理是一个关于最大公约数(或最大公约式)的定理。裴蜀定理得名于法国数学家艾蒂安·裴蜀,说明了对任何整数a、b和它们的最大公约数d
有方程有解当且仅当m是d的倍数。裴蜀等式有解时必然有无穷多个整数解,每组解x、y都称为裴蜀数,可用辗转相除法求得。
素数测试与因式分解(Miller-Rabin & Pollard-Rho)
isprime函数判断素数,Pollard-Rho在factorize中在数组里存储因子
ll mul(ll a, ll b, ll m) {
return static_cast<__int128>(a) * b % m;
}
ll power(ll a, ll b, ll m) {
ll res = 1 % m;
for (; b; b >>= 1, a = mul(a, a, m))
if (b & 1)
res = mul(res, a, m);
return res;
}
bool isprime(ll n) {
if (n < 2)
return false;
static constexpr int A[] = {2, 3, 5, 7, 11, 13, 17, 19, 23};
int s = __builtin_ctzll(n - 1);
ll d = (n - 1) >> s;
for (auto a : A) {
if (a == n)
return true;
ll x = power(a, d, n);
if (x == 1 || x == n - 1)
continue;
bool ok = false;
for (int i = 0; i < s - 1; ++i) {
x = mul(x, x, n);
if (x == n - 1) {
ok = true;
break;
}
}
if (!ok)
return false;
}
return true;
}
std::vector<ll> factorize(ll n) {
std::vector<ll> p;
std::function<void(ll)> f = [&](ll n) {
if (n <= 10000) {
for (int i = 2; i * i <= n; ++i)
for (; n % i == 0; n /= i)
p.push_back(i);
if (n > 1)
p.push_back(n);
return;
}
if (isprime(n)) {
p.push_back(n);
return;
}
auto g = [&](ll x) {
return (mul(x, x, n) + 1) % n;
};
ll x0 = 2;
while (true) {
ll x = x0,ll y = x0,ll d = 1;
ll power = 1, lam = 0;
ll v = 1;
while (d == 1) {
y = g(y);
++lam;
v = mul(v, std::abs(x - y), n);
if (lam % 127 == 0) {
d = std::gcd(v, n);
v = 1;
}
if (power == lam) {
x = y;
power *= 2;
lam = 0;
d = std::gcd(v, n);
v = 1;
}
}
if (d != n) {
f(d);
f(n / d);
return;
}
++x0;
}
};
f(n);
std::sort(p.begin(), p.end());
return p;
}博弈论(公平组合游戏(Impartial Combinatorial Games,ICG))
sg函数
其中x,y都表示某种状态,在这里表示x可以通过一次操作到y状态,mex表示一个集合中没有出现的最小数。例如,当sg(x) = 0时我们称之为必败态,相反,如果存在则称x为必胜态,说明此次存在策略使自己必定取胜,sg定理
设置x和y为ICG的状态,则:可以推广出
利用sg定理,我们就可以轻松把单一游戏的情况推广到多个子游戏组合的情况下,例如Nim游戏就是在n堆石子的异或和为0的时候必败,否则必胜。
常用于打表的函数mex函数
int mex(auto v) // v可以是vector、set等容器
{
unordered_set<int> S;
for (auto e : v)
S.insert(e);
for (int i = 0;; ++i)
if (S.find(i) == S.end())
return i;
}搜索
DFS
把根节点放进栈里 取出一个节点,进行处理 将此节点的子节点放入栈(没有子节点就不放) 判断栈是否为空。如果非空,返回第2步;如果为空,结束。
int maxn = 0x3f;
vector<int> e[maxn]; //连接关系
bool vis[maxn];
void dfs(int u){
if(结束条件) return;
vis[u] = 1; //标记已经搜索过
for (int i = 0 ;i < e[u] ;i++){
int v = e[u][i];
if(vis[v]) continue;// 已经搜索过了,剪枝
dfs(v);//下一步搜索
}
return;
}BFS
BFS的基本思路是:
把根节点放进队列里 取出一个节点,进行处理 将此节点的子节点放入队列(没有子节点就不放) 判断队列是否为空。如果非空,返回第2步;如果为空,结束。
vector<int> e[maxn]; //连接关系
bool vis[maxn];
void bfs(int x){
queue<int> q;
q.push(x);
while(!q.empty()){
int u = q.front();
q.pop();
vis[u] = 1;
for (int i = 1 ; i < e[u] ; i++){
int v = e[u][i];
if(vis[v]) continue;
q.push(v);
}
}
}快速幂
int qpow(int a, int n,int mod)
{
// a==0 && n==0 特判
int ans = 1; // n = 0 时候不进循环
while(n)
{
if(n & 1)
ans = a * ans%mod;
a = a * a%mod;
n >>= 1;
}
return ans%mod;
}字符串
KMP
1.求NEXT数组
void get_next(string b,int *next)
{
int k=-1,j=0;
next[0]=-1;
while(j<b.size())
{
if(k==-1 || b[k]==b[j])
next[++j]=++k; //next[j]=next[j-1]+1;
else k=next[k]; //k回溯
}
}2.求是否匹配
int KMP(string a,string b,int *next)
{
int i=0,j=0;
while(i<a.size())
{
if(a[i]==b[j] || j==-1) i++,j++; //相等后移
else j=next[j];
if(j==b.size()) return i-j;
else if(j>b.size()) return -1;
}
}字符串哈希
19260817 //大质数
多项式哈希函数 其中是一个素数
using std::string;
const int M = 1e9 + 7;
const int B = 233;
typedef long long ll;
int get_hash(const string& s) {
int res = 0;
for (int i = 0; i < s.size(); ++i) {
res = ((ll)res * B + s[i]) % M;
}
return res;
}
bool cmp(const string& s, const string& t) {
return get_hash(s) == get_hash(t);
}(效率低下的版本)
进制哈希
进制哈希的核心便是给出一个固定进制𝑏𝑎𝑠𝑒,将一个串的每一个元素看做一个进制位上的数字,所以这个串就可以看做一个𝑏𝑎𝑠𝑒进制的数,那么这个数就是这个串的哈希值;则我们通过比对每个串的的哈希值,即可判断两个串是否相同
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
using LL = long long;
typedef ull unsigned long long
ull base=131;
ull a[10010];
char s[10010];
int n,ans=1;
int prime=233317;
ull mod=212370440130137957ll;
ull hashe(char s[])
{
int len=strlen(s);
LL ans=0;
for (int i=0;i<len;i++)
ans=(ans*base+(ull)s[i])%mod+prime;
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%s",s);
a[i]=hashe(s);
}
sort(a+1,a+n+1);
for(int i=1;i<n;i++){
if(a[i]!=a[i+1])
ans++;
}
printf("%d",ans);
}多重哈希
#include<bits/stdc++.h>
#define FAST std::ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0)
using namespace std;
int mod1=20160817;
int mod2=19260817;
int n,ans=1;
int base=131;
struct node{
int x,y;
}a[100001];
int hash1(string s){
int sum=0;
for(int i=0;i<s.size();i++){
sum=base*sum+(int)(s[i]);
sum%=mod1;
}
return sum;
}
int hash2(string s){
int sum=0;
for(int i=0;i<s.size();i++){
sum=base*sum+(int)(s[i]);
sum%=mod2;
}
return sum;//返回hash值
}
bool sj(node x,node y){
return x.x<y.x;
}
int main(){
FAST;//优化输入输出
cin>>n;
for(int i=1;i<=n;i++){
string s;//输入字符串
cin>>s;
a[i].x=hash1(s);//给它hash值
a[i].y=hash2(s);
}
sort(a+1,a+1+n,sj);//hash值排序
for(int i=2;i<=n;i++){
if(a[i].x!=a[i-1].x||a[i].y!=a[i-1].y)ans++;
}
cout<<ans;
}字典树
const int MAXN = 500005;
int next[MAXN][26], cnt; // 用类似链式前向星的方式存图,next[i][c]表示i号点所连、存储字符为c+'a'的点的编号
void init(){ //初始化
memset(next, 0, sizeof(next)); // 全部重置为0,表示当前点没有存储字符
cnt = 1;
}
void insert(const string &s){ //插入字符串
int cur = 1;
for (auto c : s){
// 尽可能重用之前的路径,如果做不到则新建节点
if (!next[cur][c - 'a'])
next[cur][c - 'a'] = ++cnt;
cur = next[cur][c - 'a']; // 继续向下
}
} //字典树建树
bool find_prefix(const string &s) // 查找某个前缀是否出现过
{
int cur = 1;
for (auto c : s)
{
// 沿着前缀所决定的路径往下走,如果中途发现某个节点不存在,说明前缀不存在
if (!next[cur][c - 'a'])
return false;
cur = next[cur][c - 'a'];
}
return true;
}AC自动机
动态规划
线性动态规划
最长各种序列
朴素做法
#include<bits/stdc++.h>
#define ll long long
#define int ll
using namespace std;
const int maxn = 1e6 + 10;
int a[maxn], dp[maxn];
signed main()
{
ios::sync_with_stdio(false);
cin.tie();
cout.tie();
int n;
cin>>n;
for (int i = 1; i <= n; i++) {
cin>>a[i];
dp[i] = 1; //本身就是一个长度为1的子列
}
//最长上升子列
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (a[j] < a[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
//最长不下降子列
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (a[j] <= a[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
//最长下降子列
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (a[j] > a[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
//最长不上升子列
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (a[j] >= a[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
return 0;二分优化
#include<bits/stdc++.h>
#define ll long long
#define int ll
using namespace std;
const int maxn = 1e6 + 10;
int a[maxn], dp[maxn];
signed main()
{
ios::sync_with_stdio(false);
cin.tie();
cout.tie();
int n, len;
cin>>n;
for (int i = 1; i <= n; i++) {
cin>>a[i];
}
//最长上升子列
len = 0; // 最开始的最长子列长度为0
dp[0] = -1e17; //保证了第1位的数字一定能至少放在长度为0的子列后边
for (int i = 1; i <= n; i++) {
int l = 0, r = len;
while (l < r) {
int mid = (l + r + 1) / 2;
if (dp[mid] <= a[i]) {
l = mid;
} else {
r = mid - 1;
}
}
len = max(len, l + 1);
dp[l + 1] = a[i]; //不需判断二者大小 因为若原先dp[l+1]不为0 是必然大于a[i]的
}
cout<<len;//最长子列长度
//最长不下降子列
len = 0; // 最开始的最长子列长度为0
dp[0] = -1e17; //保证了第1位的数字一定能至少放在长度为0的子列后边
for (int i = 1; i <= n; i++) {
int l = 0, r = len;
while (l < r) {
int mid = (l + r + 1) / 2;
if (dp[mid] < a[i]) {
l = mid;
} else {
r = mid - 1;
}
}
len = max(len, l + 1);
dp[l + 1] = a[i]; //不需判断二者大小 因为若原先dp[l+1]不为0 是必然大于a[i]的
}
cout<<len;//最长子列长度
//最长下降子列
len = 0; // 最开始的最长子列长度为0
dp[0] = 1e17; //保证了第1位的数字一定能至少放在长度为0的子列后边
for (int i = 1; i <= n; i++) {
int l = 0, r = len;
while (l < r) {
int mid = (l + r + 1) / 2;
if (dp[mid] >= a[i]) {
l = mid;
} else {
r = mid - 1;
}
}
len = max(len, l + 1);
dp[l + 1] = a[i]; //不需判断二者大小 因为若原先dp[l+1]不为0 是必然小于a[i]的
}
cout<<len;//最长子列长度
//最长不上升子列
len = 0; // 最开始的最长子列长度为0
dp[0] = 1e17; //保证了第1位的数字一定能至少放在长度为0的子列后边
for (int i = 1; i <= n; i++) {
int l = 0, r = len;
while (l < r) {
int mid = (l + r + 1) / 2;
if (dp[mid] > a[i]) {
l = mid;
} else {
r = mid - 1;
}
}
len = max(len, l + 1);
dp[l + 1] = a[i]; //不需判断二者大小 因为若原先dp[l+1]不为0 是必然小于a[i]的
}
cout<<len;//最长子列长度
return 0;背包问题
01背包
一个物品只能取一次
#include <bits/stdc++.h>
using namespace std;
const int N = 110, M = 1010;
int n, m, v[N], w[N]; // n-物品种数 m-背包容积 v[i]-i号物品的体积、w[i]-i号物品的价值
int f[M];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> m >> n;
for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
for (int i = 1; i <= n; ++ i) {
for (int j = m; j >= v[i]; -- j) { // 注意j的遍历顺序
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[m] << '\n';
return 0;
}完全背包
有无数个物品,可以任意取
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e4, M = 1e7;
ll n, m, v[N], w[N]; // n-物品种数 m-背包容积 v[i]-i号物品的体积、w[i]-i号物品的价值
ll f[M];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> m >> n;
for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
for (int i = 1; i <= n; ++ i) {
for (int j = v[i]; j <= m; ++ j) { // 注意j的遍历顺序
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[m] << '\n';
return 0;
}分组背包
有⼀些物品和⼀个容积为的背包,把物品分成n组,其中第组共 种物品,第种物品的体积为,价值为,
每组中只能选择⼀个物品,要求从组中选出若⼲物品使其总价值最⼤且总体积不超过背包容积。
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 110;
int s[M], v[M][N], w[M][N];
int f[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> m >> n;
for (int i = 1; i <= n; ++ i) {
int a, b, c;
cin >> a >> b >> c;
++ s[c];
v[c][s[c]] = a, w[c][s[c]] = b;
}
for (int i = 1; i <= n; ++ i)
for (int j = m; j >= 0; -- j)
for (int k = 1; k <= s[i]; ++ k)
if (j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << '\n';
return 0;
}多重背包
有种物品和⼀个容积为 的背包,第种物品的体积为 ,价值为,共个,要求从种物品中
取出若⼲使其总价值最⼤且总体积不超过背包容积.
朴素做法
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 4e4 + 10;
int v[N], w[N], s[N], f[M];
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++ i) cin >> w[i] >> v[i] >> s[i];
for (int i = 1; i <= n; ++ i)
for (int k = 1; k <= s[i]; ++ k)
for (int j = m; j >= v[i]; -- j)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << '\n';
return 0;
}二进制拆分优化
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int n,C,dp[N];
int w[N],c[N],m[N];
int new_n; //⼆进制拆分后的新物品总数量
int new_w[N],new_c[N],new_m[N]; //⼆进制拆分后新物品
int main(){
cin >> n >>C;
for(int i=1;i<=n;i++) cin>>w[i]>>c[i]>>m[i];
//以下是⼆进制拆分
int new_n = 0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m[i];j<<=1) { //⼆进制枚举:1,2,4...
m[i]-=j; //减去已拆分的
new_c[++new_n] = j*c[i]; //新物品
new_w[new_n] = j*w[i];
}
if(m[i]){ //最后⼀个是余数
new_c[++new_n] = m[i]*c[i];
new_w[new_n] = m[i]*w[i];
}
}
//以下是滚动数组版本的0/1背包
for(int i=1;i<=new_n;i++) //枚举物品
for(int j=C;j>=new_c[i];j--) //枚举背包容量
dp[j] = max(dp[j],dp[j-new_c[i]]+new_w[i]);
cout << dp[C] << endl;
return 0;区间dp
区间类型动态规划是线性动态规划的拓展,它在分阶段划分问题时,与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系.例如,区间类动态规划的特点:
合并:即将两个或多个部分进行整合。
特征:能将问题分解成为两两合并的形式。
求解:对整个问题设最优值,枚举合并点,将问题分解成为左右两个部分,最后将左右两个部分的最优值进行合并得到原问题的最优值。
区间dp的做法比较固定,即枚举区间长度,再枚举左端点,之后枚举端点的断点进行转移
#include<bits/stdc++.h> using std::cin,std::cout,std::deque,std::pair,std::queue,std::vector; #define int long long #define inf 0x3f3f3f3f int qpow(int a, int n,int mod = 1e9 + 7){ int ans = 1; while(n){if(n & 1){ans = a * ans%mod;}a = a * a%mod;n >>= 1;}return ans%mod; } // int head[N],cnt; // struct edge{ // int to,nxt,val; // }e[N]; // int add(int u,int v){ // e[++cnt].to = v; // e[cnt].nxt = head[u]; // head[u] = cnt; // } const int N = 210; int a[2*N]; int dpmax[N][N]; int dpmin[N][N]; int sum[N]; void solve(){ int n; cin >> n; for(int i = 1;i <= n;i++){ cin >> a[i]; a[i + n] = a[i]; } for(int i = 1;i <= 2*n;i++){ sum[i] = sum[i - 1] + a[i]; } for(int len = 2;len <= n;len++){ for(int l = 1;l < 2*n - len + 1;l++){ int r = len + l - 1; dpmin[l][r] = inf,dpmax[l][r] = 0; for(int k = l;k <= r;k++){ dpmin[l][r] = std::min(dpmin[l][k] + dpmin[k + 1][r],dpmin[l][r]); dpmax[l][r] = std::max(dpmax[l][k] + dpmax[k + 1][r],dpmax[l][r]); } dpmin[l][r] += sum[r] - sum[l - 1]; dpmax[l][r] += sum[r] - sum[l - 1]; } } int max = 0,min = inf; for(int i = 1;i <= n;i++){ min = std::min(dpmin[i][n + i - 1],min); max = std::max(dpmax[i][n + i - 1],max); } cout << min << '\n' << max << '\n'; } signed main(){ std::ios::sync_with_stdio(false); cin.tie(0); int T; T = 1; //cin >> T; while(T--){ solve(); } }
树形dp
两种方向
- 1.根->叶(往往是在从叶往根dfs一遍之后(相当于预处理),再重新往下获取最后的答案。 )
- 2.叶->根(在回溯的时候从叶子节点往上更新信息)
难点
- 1.利用递归+记忆化搜索
- 2.细节多,从子树,从父亲,从兄弟,.......,有小的要处理的地方,脑子不清晰的时候做起来颇为恶心
- 状态表示和转移方程,也是真正难的地方。做到后面,树形DP的老套路都也就那么多,难的还是怎么能想出转移方程,各种DP做到最后都是这样!
状压dp
状压dp就是将状态压缩成二进制进行保存,是利用计算机二进制的性质来描述状态的一种dp方式。
泰难
数位dp
数位dp有个通用的套路,就是先采用前缀和思想,将求解“[𝑙,𝑟]这个区间内的满足约束的数的数量”,转化为“[1,𝑟]满足约束的数量 - 区间[1,𝑙−1]满足约束的数量。
所以我们最终要求解的问题通通转化为:[1,𝑥]中满足约束的数量,或者[0,𝑥]中的满足约束的数量(左边界取决于题目),然后将数字𝑥拆分为一个个数位
LL solve(LL x)
{
int len = 0;
while(x > 0)
{
a[++ len] = x % 10;
x /= 10;
}
return dfs(...); //记忆化搜索
}求解区间,常常分解成之和
用dfs写法,用形参pos来表示当前枚举的位置,一般从高到低。
举例:假设x为4132,用“?”来表示暂未填写的数位,则现在填数状态为????,第一步我们得先填写第len位(最高位),我们只能填写0~4
若填写大于4的数码,显然不在我们的枚举范围里
如果填写4的话下面的数字还是会受到限制,下面的数字就不能填超过1的数字
如果填写0~3的话,剩下的数字就可以随便填写了,所以我们需要记录一个变量,表示在当前数位上是不是可以随意填写。
limit : bool值变量,表示枚举的第pos位是否受限制。该位为true表示取得数不能大于,只有当的位置填写的数都等于时,该值才为,否则表示当前位没有限制,可以取到[0,R - 1],R - 1表示在R进制下最多能取到的数字。
当我们搜索到的时候,表示所有数位都已经填写完毕了,每个“?”都被替换成了具体的数字,这可以作为一个递归边界,我们需要返回枚举填写的所有数位和sum,故dfs函数的形参还得添加:sum
sum: int型变量,表示当前的数位和。以上是普通的dfs搜索,而数位dp就是把相同的部分给去掉了
设置状态
LL dfs(int pos, bool limit, int sum)
{
if(!pos) //递归边界
return sum;
if(!limit && ~f[pos][sum]) //没限制并且dp值已搜索过
return f[pos][sum];
int up = limit ? a[pos] : 9; //
LL res = 0;
for(int i = 0; i <= up; i ++)
res = (res + dfs(pos - 1, limit && i == up, sum + i)) % md;
if(!limit) //记搜,可复用
f[pos][sum] = res;
return res;
}记忆化dfs函数常见形参
- :int型变量,表示当前枚举的位置,一般从高到低
𝑙𝑖𝑚𝑖𝑡:bool型变量,表示枚举的第𝑝𝑜𝑠位是否受到限制,
为true表示取的数不能大于𝑎[𝑝𝑜𝑠],而只有在[𝑝𝑜𝑠+1,𝑙𝑒𝑛]的位置上填写的数都等于𝑎[𝑖]时该值才为true
否则表示当前位没有限制,可以取到[0,𝑅−1],因为𝑅进制的数中数位最多能取到的就是𝑅−1
- 𝑙𝑎𝑠𝑡:int型变量,表示上一位(第𝑝𝑜𝑠+1位)填写的值,往往用于约束了相邻数位之间的关系的题目
- 𝑙𝑒𝑎𝑑0:bool型变量,表示是否有前导零,即在𝑙𝑒𝑛→(𝑝𝑜𝑠+1)这些位置是不是都是前导零
基于常识,我们往往默认一个数没有前导零,也就是最高位不能为0,即不会写为000123,而是写为123
只有没有前导零的时候,才能计算0的贡献。
那么前导零何时跟答案有关?
- 统计0的出现次数
- 相邻数字的差值
- 以最高位为起点确定的奇偶位
- 𝑠𝑢𝑚:int型变量,表示当前𝑙𝑒𝑛→(𝑝𝑜𝑠+1)的数位和
- 𝑟:int型变量,表示整个数前缀取模某个数𝑚的余数
- 该参数一般会用在:约束中出现了能被𝑚整除
- 当然也可以拓展为数位和取模的结果
- 𝑠𝑡:int型变量,用于状态压缩,对一个集合的数在数位上的出现次数的奇偶性有要求时,其二进制形式就可以表示每个数出现的奇偶性
数据结构
并查集
常规并查集
int f[N],d[N];
int find(int x){
if(x == f[x]) return x;
else return f[x] = find(f[x]);
}
int add(int x,int y){
int fx = find(x),fy = find(y);
if(fx != fy) f[fy] = fx;
}带权并查集
带权并查集可以存储节点的权值
int FindSet(int x) {
if (x == parent[x])
return x;
else {
int t = parent[x]; //记录原父节点编号
parent[x] = FindSet(parent[x]); //父节点变为根节点,此时value[x]=父节点到根节点的权值
value[x] += value[t]; //当前节点的权值加上原本父节点的权值
return parent[x]
}
}因为在路径压缩后父节点直接变为根节点,此时父节点的权值已经是父节点到根节点的权值了,将当前节点的权值加上原本父节点的权值,就得到当前节点到根节点的权值
int merge(int x,int y,int s){
int xRoot = findSet(x);
int yRoot = findSet(y);
if(xRoot != yRoot){
parent[xRoot] = yRoot;
value[xRoot] = -value[x] + value[y] + s;
}
}st表
形成
int f[MAXN][21]; // 第二维的大小根据数据范围决定,不小于log(MAXN)
for (int i = 1; i <= n; ++i)
f[i][0] = read(); // 读入数据
for (int i = 1; i <= 20; ++i)
for (int j = 1; j + (1 << i) - 1 <= n; ++j)
f[j][i] = max(f[j][i - 1], f[j + (1 << (i - 1))][i - 1]);原理如图
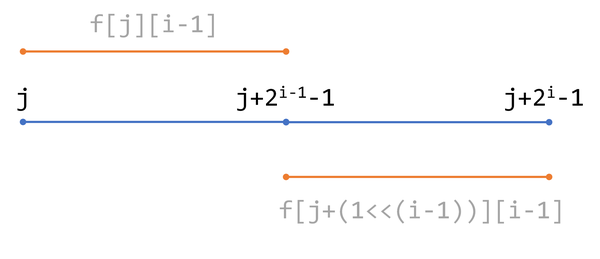
img
递推log
for (int i = 2; i <= n; ++i)
Log2[i] = Log2[i / 2] + 1;在线查询
for (int i = 0; i < m; ++i)
{
int l = read(), r = read();
int s = Log2[r - l + 1];
printf("%d\n", max(f[l][s], f[r - (1 << s) + 1][s]));
}模板
int A[N], f[__lg(N) + 1][N];
void init(int n) {
for (int i = 1; i <= n; ++i)
f[0][i] = A[i];
for (int i = 1; i <= __lg(n); ++i)
for (int j = 1; j + (1 << i) - 1 <= n; ++j)
f[i][j] = max(f[i - 1][j], f[i - 1][j + (1 << (i - 1))]);
}
int query(int l, int r) {
int s = __lg(r - l + 1);
return max(f[s][l], f[s][r - (1 << s) + 1]);
}链式前向星
int head[N],cnt;
struct edge{
int to,nxt,val;
}e[N];
int add(int u,int v){
e[++cnt].to = v;
e[cnt].nxt = head[u];
head[u] = cnt;
}链式前向星的遍历
BFS
void bfs(int u) ///队列实现广度优先搜索 { queue<int>q; vis[u]=true; q.push(u); while(!q.empty()){ int k=q.front(); q.pop(); printf("%d ",k); for(int i=head[k];~i;i=edge[i].next){ int to=edge[i].to; if(!vis[to]){ q.push(to); vis[to]=true; ///因为不是递归实现,所以每次放入队列后都需要立即标记。 } } } }DFS
void dfs(int u) ///递归实现深度优先搜索 { printf("%d ",u); vis[u]=true; for(int i=head[u];i;i=edge[i].next){ int to=edge[i].to; if(!vis[to]){ dfs(to); } } }
树状数组
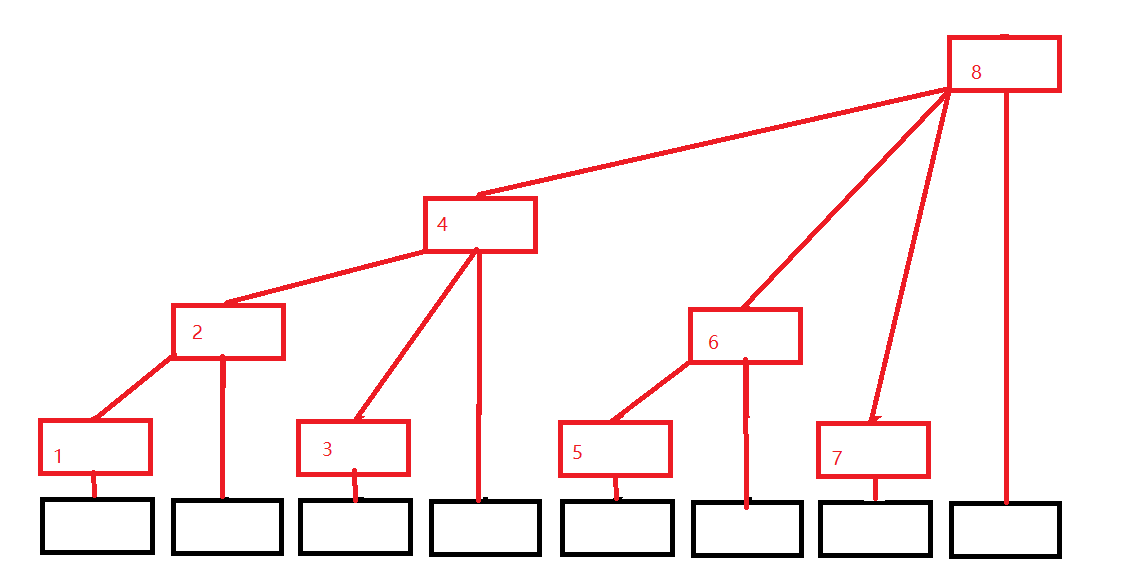
img
黑色数组代表原来的数组(下面用A[i]代替),红色结构代表我们的树状数组(下面用C[i]代替),每个位置只有一个方框,令每个位置存的就是子节点的值的和,则有
我们要找前7项和,那么应该是;
int n;
int a[1005],c[1005];
int lowbit(int x){
return x&(-x);
}
void updata(int i,int k){
while(i <= n){
c[i] += k;
i += lowbit(i);
}
}
int getsum(int i){
int res = 0;
while(i > 0){
res += c[i];
i -= lowbit(i);
}
return res;
}单点修改,区间查询
void solve(){
cin >> n >> m;
for(int i = 1;i <= n;i++){
int a;
cin >> a;
updata(i,a);
}
for(int i = 1;i <= m;i++){
int op,x,y;
cin >> op >> x >> y;
if(op == 1) updata(x,y);
if(op == 2) cout << getsum(y) - getsum(x -1) << '\n';
}
}
signed main(){
// std::ios::sync_with_stdio(false);
// cin.tie(0);
int T;
T = 1;
//cin >> T;
while(T--){
solve();
}
}区间修改,单点查询
区间修改需要用树状数组来存储差分数组,在树状数组的两端进行差分数组的修改,求和时直接求差分数组的前缀和就可以得到修改之后的数据点上的值
void solve(){
cin >> n >> m;
for(int i = 1;i <= n;i++){
cin >> a[i];
updata(i,a[i] - a[i - 1]);
}
for(int i = 1;i <= m;i++){
int op;
cin >> op;
if(op == 1){
int x,y,k;
cin >> x >> y >> k;
updata(x,k);
updata(y + 1,-k);
}
if(op == 2){
int x;
cin >> x;
cout << getsum(x) << '\n';
}
}
}线段树
线段树的基本结构和建树
线段树将每个长度不为的区间划分成左右两个区间递归求解,把整个线段划分为一个树形结构,通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作.
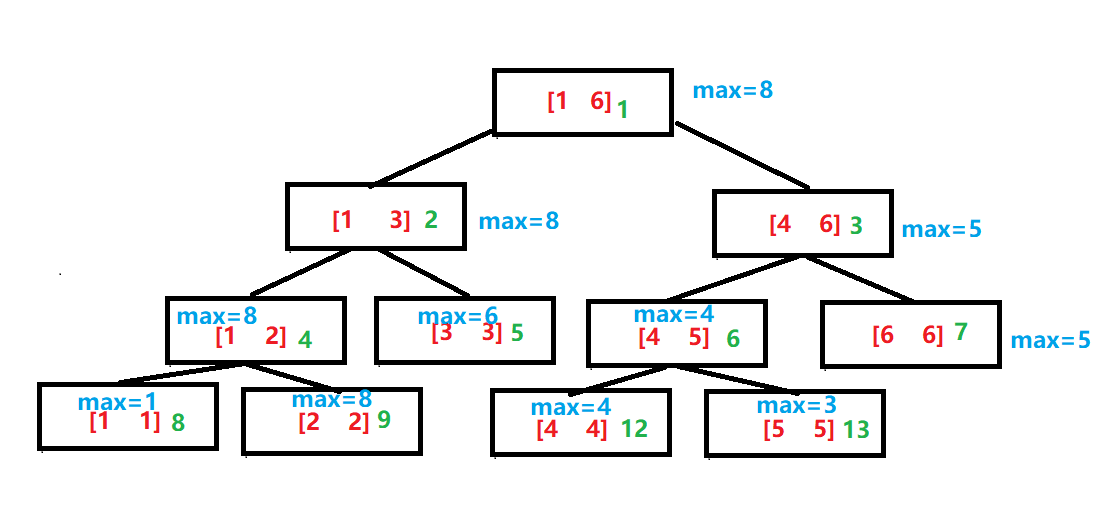
img
对于A[1:6] = {1,8,6,4,3,5}来说,线段树如上所示,红色代表每个结点存储的区间,蓝色代表该区间最值,绿色代表区间的下标。
可以发现,每个叶子结点的值就是数组的值,每个非叶子结点的度都为二,且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。设父亲节点的下标为,左儿子的下标为,右儿子节点下标为,易得,因此线段树建树需要4*n的空间。
我们通常通过来寻找左孩子,通过来寻找右孩子
以下模板求的是区间最大值
区间最大值模板
const int maxn = 100005;
int a[maxn],t[maxn<<2]; //a为原来区间,t为线段树
void Pushup(int k){ //更新函数,这里是实现最大值 ,同理可以变成,最小值,区间和等
t[k] = max(t[k<<1],t[k<<1|1]);
}
//递归方式建树 build(1,1,n);
void build(int k,int l,int r){ //k为当前需要建立的结点,l为当前需要建立区间的左端点,r则为右端点
if(l == r) //左端点等于右端点,即为叶子节点,直接赋值即可
t[k] = a[l];
else{
int m = l + ((r-l)>>1); //m则为中间点,左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
build(k<<1,l,m); //递归构造左儿子结点
build(k<<1|1,m+1,r); //递归构造右儿子结点
Pushup(k); //更新父节点
}
}
//递归方式更新 updata(p,v,1,n,1);【点更新】
void updata(int p,int v,int l,int r,int k){ //p为下标,v为要加上的值,l,r为结点区间,k为结点下标
if(l == r) //左端点等于右端点,即为叶子结点,直接加上v即可
a[k] += v,t[k] += v; //原数组和线段树数组都得到更新
else{
int m = l + ((r-l)>>1); //m则为中间点,左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
if(p <= m) //如果需要更新的结点在左子树区间
updata(p,v,l,m,k<<1);
else //如果需要更新的结点在右子树区间
updata(p,v,m+1,r,k<<1|1);
Pushup(k); //更新父节点的值
}
}
//递归方式区间查询 query(L,R,1,n,1);
int query(int L,int R,int l,int r,int k){ //[L,R]即为要查询的区间,l,r为结点区间,k为结点下标
if(L <= l && r <= R) //如果当前结点的区间真包含于要查询的区间内,则返回结点信息且不需要往下递归
return t[k];
else{
int res = -INF; //返回值变量,根据具体线段树查询的什么而自定义
int mid = l + ((r-l)>>1); //m则为中间点,左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
if(L <= m) //如果左子树和需要查询的区间交集非空
res = max(res, query(L,R,l,m,k<<1));
if(R > m) //如果右子树和需要查询的区间交集非空,注意这里不是else if,因为查询区间可能同时和左右区间都有交集
res = max(res, query(L,R,m+1,r,k<<1|1));
return res; //返回当前结点得到的信息
}
}
void Pushdown(int k){ //更新子树的lazy值,这里是RMQ的函数,要实现区间和等则需要修改函数内容
if(lazy[k]){ //如果有lazy标记
lazy[k<<1] += lazy[k]; //更新左子树的lazy值
lazy[k<<1|1] += lazy[k]; //更新右子树的lazy值
t[k<<1] += lazy[k]; //左子树的最值加上lazy值
t[k<<1|1] += lazy[k]; //右子树的最值加上lazy值
lazy[k] = 0; //lazy值归0
}
}
//递归更新区间 updata(L,R,v,1,n,1);【区间更新】
void updata(int L,int R,int v,int l,int r,int k){ //[L,R]即为要更新的区间,l,r为结点区间,k为结点下标
if(L <= l && r <= R){ //如果当前结点的区间真包含于要更新的区间内
lazy[k] += v; //懒惰标记
t[k] += v; //最大值加上v之后,此区间的最大值也肯定是加v
}
else{
Pushdown(k); //重难点,查询lazy标记,更新子树
int m = l + ((r-l)>>1);
if(L <= m) //如果左子树和需要更新的区间交集非空
update(L,R,v,l,m,k<<1);
if(m < R) //如果右子树和需要更新的区间交集非空
update(L,R,v,m+1,r,k<<1|1);
Pushup(k); //更新父节点
}
}
//递归方式区间查询 query(L,R,1,n,1);
int query(int L,int R,int l,int r,int k){ //[L,R]即为要查询的区间,l,r为结点区间,k为结点下标
if(L <= l && r <= R) //如果当前结点的区间真包含于要查询的区间内,则返回结点信息且不需要往下递归
return t[k];
else{
Pushdown(k); /**每次都需要更新子树的Lazy标记*/
int res = -INF; //返回值变量,根据具体线段树查询的什么而自定义
int mid = l + ((r-l)>>1); //m则为中间点,左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
if(L <= m) //如果左子树和需要查询的区间交集非空
res = max(res, query(L,R,l,m,k<<1));
if(R > m) //如果右子树和需要查询的区间交集非空,注意这里不是else if,因为查询区间可能同时和左右区间都有交集
res = max(res, query(L,R,m+1,r,k<<1|1));
return res; //返回当前结点得到的信息
}
}区间和模板
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int MAXN = 1e5 + 5;
ll tree[MAXN << 2], mark[MAXN << 2], n, m, A[MAXN];
void push_down(int p, int len) //下传标记
{
if (len <= 1) return;
tree[p << 1] += mark[p] * (len - len / 2);
mark[p << 1] += mark[p];
tree[p << 1 | 1] += mark[p] * (len / 2);
mark[p << 1 | 1] += mark[p];
mark[p] = 0;
}
void build(int p = 1, int cl = 1, int cr = n) //建树
{
if (cl == cr) return void(tree[p] = A[cl]);
int mid = (cl + cr) >> 1;
build(p << 1, cl, mid);
build(p << 1 | 1, mid + 1, cr);
tree[p] = tree[p << 1] + tree[p << 1 | 1];
}
ll query(int l, int r, int p = 1, int cl = 1, int cr = n) //查询l到r的区间和
{
if (cl >= l && cr <= r) return tree[p];
push_down(p, cr - cl + 1);
ll mid = (cl + cr) >> 1, ans = 0;
if (mid >= l) ans += query(l, r, p << 1, cl, mid);
if (mid < r) ans += query(l, r, p << 1 | 1, mid + 1, cr);
return ans;
}
void update(ll l, ll r, ll d, ll p = 1, ll cl = 1, ll cr = n)
{
if (cl > r || cr < l) return;
else if (cl >= l && cr <= r){
tree[p] += (cr - cl + 1) * d;
if (cr > cl) mark[p] += d;
}
else{
ll mid = (cl + cr) / 2;
push_down(p, cr - cl + 1);
update(l, r, d, p * 2, cl, mid);
update(l, r, d, p * 2 + 1, mid + 1, cr);
tree[p] = tree[p * 2] + tree[p * 2 + 1];
}
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 1; i <= n; ++i)
cin >> A[i];
build();
while (m--)
{
int o, l, r, d;
cin >> o >> l >> r;
if (o == 1)
cin >> d, update(l, r, d);
else
cout << query(l, r) << '\n';
}
return 0;
}区间加,乘
#include <bits/stdc++.h>
#define MAXN 100010
#define ll long long
using namespace std;
int n, m, mod;
int a[MAXN];
struct Segment_Tree {
ll sum, add, mul;
int l, r;
}s[MAXN * 4];
void update(int pos) {
s[pos].sum = (s[pos << 1].sum + s[pos << 1 | 1].sum) % mod;
return;
}
void pushdown(int pos) { //pushdown的维护
s[pos << 1].sum = (s[pos << 1].sum * s[pos].mul + s[pos].add * (s[pos << 1].r - s[pos << 1].l + 1)) % mod;
s[pos << 1 | 1].sum = (s[pos << 1 | 1].sum * s[pos].mul + s[pos].add * (s[pos << 1 | 1].r - s[pos << 1 | 1].l + 1)) % mod;
s[pos << 1].mul = (s[pos << 1].mul * s[pos].mul) % mod;
s[pos << 1 | 1].mul = (s[pos << 1 | 1].mul * s[pos].mul) % mod;
s[pos << 1].add = (s[pos << 1].add * s[pos].mul + s[pos].add) % mod;
s[pos << 1 | 1].add = (s[pos << 1 | 1].add * s[pos].mul + s[pos].add) % mod;
s[pos].add = 0;
s[pos].mul = 1;
return;
}
void build_tree(int pos, int l, int r) { //建树
s[pos].l = l;
s[pos].r = r;
s[pos].mul = 1;
if (l == r) {
s[pos].sum = a[l] % mod;
return;
}
int mid = (l + r) >> 1;
build_tree(pos << 1, l, mid);
build_tree(pos << 1 | 1, mid + 1, r);
update(pos);
return;
}
void ChangeMul(int pos, int x, int y, int k) { //区间乘法
if (x <= s[pos].l && s[pos].r <= y) {
s[pos].add = (s[pos].add * k) % mod;
s[pos].mul = (s[pos].mul * k) % mod;
s[pos].sum = (s[pos].sum * k) % mod;
return;
}
pushdown(pos);
int mid = (s[pos].l + s[pos].r) >> 1;
if (x <= mid) ChangeMul(pos << 1, x, y, k);
if (y > mid) ChangeMul(pos << 1 | 1, x, y, k);
update(pos);
return;
}
void ChangeAdd(int pos, int x, int y, int k) { //区间加法
if (x <= s[pos].l && s[pos].r <= y) {
s[pos].add = (s[pos].add + k) % mod;
s[pos].sum = (s[pos].sum + k * (s[pos].r - s[pos].l + 1)) % mod;
return;
}
pushdown(pos);
int mid = (s[pos].l + s[pos].r) >> 1;
if (x <= mid) ChangeAdd(pos << 1, x, y, k);
if (y > mid) ChangeAdd(pos << 1 | 1, x, y, k);
update(pos);
return;
}
ll AskRange(int pos, int x, int y) { //区间询问
if (x <= s[pos].l && s[pos].r <= y) {
return s[pos].sum;
}
pushdown(pos);
ll val = 0;
int mid = (s[pos].l + s[pos].r) >> 1;
if (x <= mid) val = (val + AskRange(pos << 1, x, y)) % mod;
if (y > mid) val = (val + AskRange(pos << 1 | 1, x, y)) % mod;
return val;
}
int main() {
cin >> n >> m >> mod;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
build_tree(1, 1, n);
for (int i = 1; i <= m; i++) {
int opt, x, y;
cin >> opt >> x >> y;
if (opt == 1) {
int k;
cin >> k;
ChangeMul(1, x, y, k);
}
if (opt == 2) {
int k;
cin >> k;
ChangeAdd(1, x, y, k);
}
if (opt == 3) {
cout << AskRange(1,x,y);
}
}
return 0;
}zkw线段树
理论上能放的数,只能查询的范围
非递归方式建树,建的是一个满二叉树
int N = 1 << __lg(n + 5) + 1;
vector<int> tree(N << 1);
for (int i = 1; i <= n; ++i)
tree[i + N] = A[i];
for (int i = N; i; --i)
tree[i] = tree[i << 1] + tree[i << 1 | 1];单点修改
void update(int x, int d)
{
for (int i = x + N; i; i >>= 1)
tree[i] += d;
}区间查询
int query(int l, int r)
{
int ans = 0;
for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
{
if (~l & 1) ans += tree[l ^ 1]; // 左端点是左儿子
if (r & 1) ans += tree[r ^ 1]; // 右端点是右儿子
}
return ans;
}区间修改
void update(int l, int r, int d)
{
int len = 1, cntl = 0, cntr = 0; // cntl、cntr是左、右两边分别实际修改的区间长度
for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1, len <<= 1)
{
tree[l] += cntl * d, tree[r] += cntr * d;
if (~l & 1) tree[l ^ 1] += d * len, mark[l ^ 1] += d, cntl += len;
if (r & 1) tree[r ^ 1] += d * len, mark[r ^ 1] += d, cntr += len;
}
for (; l; l >>= 1, r >>= 1)
tree[l] += cntl * d, tree[r] += cntr * d;
}区间修改的查询
int query(int l, int r)
{
int ans = 0, len = 1, cntl = 0, cntr = 0;
for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1, len <<= 1)
{
ans += cntl * mark[l] + cntr * mark[r];
if (~l & 1) ans += tree[l ^ 1], cntl += len;
if (r & 1) ans += tree[r ^ 1], cntr += len;
}
for (; l; l >>= 1, r >>= 1)
ans += cntl * mark[l] + cntr * mark[r];
return ans;
}区间加,区间查询最大值的模板
void update(int l, int r, int d) {
for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
{
if (l < N) tree[l] = max(tree[l << 1], tree[l << 1 | 1]) + mark[l],
tree[r] = max(tree[r << 1], tree[r << 1 | 1]) + mark[r];
if (~l & 1) tree[l ^ 1] += d, mark[l ^ 1] += d;
if (r & 1) tree[r ^ 1] += d, mark[r ^ 1] += d;
}
for (; l; l >>= 1, r >>= 1)
if (l < N) tree[l] = max(tree[l << 1], tree[l << 1 | 1]) + mark[l],
tree[r] = max(tree[r << 1], tree[r << 1 | 1]) + mark[r];
};
int query(int l, int r) {
int maxl = -INF, maxr = -INF;
for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
{
maxl += mark[l], maxr += mark[r];
if (~l & 1) cmax(maxl, tree[l ^ 1]);
if (r & 1) cmax(maxr, tree[r ^ 1]);
}
for (; l; l >>= 1, r >>= 1)
maxl += mark[l], maxr += mark[r];
return max(maxl, maxr);
};struct seg{
ll o[1 << 20];int L;
void upt(int x){
o[x] = o[x << 1] + o[x << 1|1];
}
void init(int n,int *w){
L = 2 << std::__lg(n + 1);
for(int i = 1;i <= n;i++) o[L + i] = w[i];
for(int i = L;i >= 1;--i) upt(i);
}
void upt(int p,int v){
for(o[p += L] += v;p >>= 1;upt(p));
}
ll qry(int l,int r){
l += L - 1,r += L + 1;
ll ans = 0;
for(;l^r^1;l >>=1,r>>=1){
if((l&1) == 0) ans += o[l^1];
if((r&1) == 0) ans += o[r^1];
}
}
ll qry2(int l,int r){
if(l == r) return o[l + L];
ll le = o[l + L],ri = o[r + L];
l += L,r += L;
for(;l^r^1;l >>= 1,r >>= 1){
if((l&1) == 0) le = le + o[l^1];
if((r&1) == 1) ri = o[r^1] + ri;
}
return le + ri;
}
}sgt; (不含区间查询)扫描线(不太理解modify部分)
#include<bits/stdc++.h>
using std::cin,std::cout,std::deque,std::pair,std::queue,std::vector;
using LL = long long;
#define inf 0x3f3f3f3f
int qpow(int a, int n,int mod = 1e9 + 7){
int ans = 1; while(n){if(n & 1){ans = a * ans%mod;}a = a * a%mod;n >>= 1;}return ans%mod;
}
// int head[N],cnt;
// struct edge{
// int to,nxt,val;
// }e[N];
// int add(int u,int v){
// e[++cnt].to = v;
// e[cnt].nxt = head[u];
// head[u] = cnt;
// }
const int N = 2e5 + 10;
int v[N];
struct l{
int x,y1,y2,state;
bool operator<(l a){
return x < a.x;
}
}line[N];
struct node{
int l,r;
long long len;
int cover;
}sgt[N<<3];
inline int ls(int k){
return k<<1;
}
inline int rs(int k){
return k<<1|1;
}
inline void pushup(int k){
if(sgt[k].cover) sgt[k].len = sgt[k].r - sgt[k].l;
else sgt[k].len = sgt[ls(k)].len + sgt[rs(k)].len;
}
void built(int l,int r,int k = 1){
sgt[k].l = v[l],sgt[k].r = v[r];
if(r - l <= 1) return;
int m = (l + r)>>1;
built(l,m,ls(k));
built(m,r,rs(k));
}
void modify(int x,int y,int z,int k = 1){
int l = sgt[k].l,r = sgt[k].r;
if(x <= l&&y >= r){
sgt[k].cover+=z;
pushup(k);
return;
}
if(x < sgt[ls(k)].r) modify(x,y,z,ls(k));
if(y > sgt[rs(k)].l) modify(x,y,z,rs(k));
pushup(k);
}
void solve(){
int n;
cin >> n;
int a,b,c,d;
for(int i = 1;i <= n;i++){
cin >> a >> b >> c >> d;
v[i] = b,v[i + n] = d;
line[i] = (l){a,b,d,1},line[i + n] = (l){c,b,d,-1};
}
std::sort(v + 1,v + 1 + (n << 1));
std::sort(line + 1,line + 1 + (n << 1));
built(1,n<<1);
unsigned long long ans = 0;
for(int i = 1;i <= (n << 1);i++){
ans += sgt[1].len*(line[i].x - line[i - 1].x);
modify(line[i].y1,line[i].y2,line[i].state);
}
cout << ans << '\n';
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
// cin >> T;
while(T--){
solve();
}
}莫队
如果能在中从的答案转移到这四个与之紧邻的区间的答案,则可以考虑使用莫队
例题:给出一个序列和若干查询l,r,问[l,r]中有多少个不同的数。
优化1
在q1和q2两个区间内进行指针的左右移动,如果左指针在查询区间左边,左指针右移,如果左指针在查询左区间右边,左指针右移,如果右指针在查询右端点右边,右指针左移,否则右移。
int aa[maxn], cnt[maxn], l = 1, r = 0, now = 0; //每个位置的数值、每个数值的计数器、左指针、右指针、当前统计结果(总数)
void add(int pos) {//添加一个数
if(!cnt[aa[pos]]) ++now;//在区间中新出现,总数要+1
++cnt[aa[pos]];
}
void del(int pos) {//删除一个数
--cnt[aa[pos]];
if(!cnt[aa[pos]]) --now;//在区间中不再出现,总数要-1
}
void work() {//优化2主过程
for(int i = 1; i <= q; ++i) {//对于每次询问
int ql, qr;
scanf("%d%d", &ql, &qr);//输入询问的区间
while(l < ql) del(l++);//如左指针在查询区间左方,左指针向右移直到与查询区间左端点重合
while(l > ql) add(--l);//如左指针在查询区间左端点右方,左指针左移
while(r < qr) add(++r);//右指针在查询区间右端点左方,右指针右移
while(r > qr) del(r--);//否则左移
printf("%d\n", now);//输出统计结果
}
}优化2
预处理
把大小为n的序列分成个块,从编号,然后根据这个对查询区间进行排序。一种方法是把查询区间按照左端点所在的块进行排序,如果左端点所在块相同,再按照右端点排序。排完序后我们再进行左右指针跳来跳去的操作
int cmp(query a, query b) {
return belong[a.l] == belong[b.l] ? a.r < b.r : belong[a.l] < belong[b.l];
}#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
#define maxn 1010000
#define maxb 1010
int aa[maxn], cnt[maxn], belong[maxn];
int n, m, size, bnum, now, ans[maxn];
struct query {
int l, r, id;
} q[maxn];
int cmp(query a, query b) {
return (belong[a.l] ^ belong[b.l]) ? belong[a.l] < belong[b.l] : ((belong[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
#define isdigit(x) ((x) >= '0' && (x) <= '9')
int read() {
int res = 0;
char c = getchar();
while(!isdigit(c)) c = getchar();
while(isdigit(c)) res = (res << 1) + (res << 3) + c - 48, c = getchar();
return res;
}
void printi(int x) {
if(x / 10) printi(x / 10);
putchar(x % 10 + '0');
}
int main() {
scanf("%d", &n);
size = sqrt(n);
bnum = ceil((double)n / size);
for(int i = 1; i <= bnum; ++i)
for(int j = (i - 1) * size + 1; j <= i * size; ++j) {
belong[j] = i;
}
for(int i = 1; i <= n; ++i) aa[i] = read();
m = read();
for(int i = 1; i <= m; ++i) {
q[i].l = read(), q[i].r = read();
q[i].id = i;
}
sort(q + 1, q + m + 1, cmp);
int l = 1, r = 0;
for(int i = 1; i <= m; ++i) {
int ql = q[i].l, qr = q[i].r;
while(l < ql) now -= !--cnt[aa[l++]];
while(l > ql) now += !cnt[aa[--l]]++;
while(r < qr) now += !cnt[aa[++r]]++;
while(r > qr) now -= !--cnt[aa[r--]];
ans[q[i].id] = now;
}
for(int i = 1; i <= m; ++i) printi(ans[i]), putchar('\n');
return 0;
}图论
基础概念
在
简单图
自环
重边
在无向图中和算一组重边,而在有向图中,和不为重边。
简单图
简单图 (simple graph):若一个图中没有自环和重边,它被称为简单图。具有至少两个顶点的简单无向图中一定存在度相同的结点。
拓扑排序
int deg[MAXN], A[MAXN];
bool toposort(int n)
{
int cnt = 0;
queue<int> q;
for (int i = 1; i <= n; ++i)
if (deg[i] == 0)
q.push(i);
while (!q.empty())
{
int t = q.front();
q.pop();
A[cnt++] = t;
for (auto to : edges[t])
{
deg[to]--;
if (deg[to] == 0) // 出现了新的入度为0的点
q.push(to);
}
}
return cnt == n;
}单元最短路径问题(SSSP)
(x,y,z)描述x出发到达y且长度为z的有向边,dist[i]表示从起点1到节点i的最短路径的长度
Dijkstra算法
1.初始化dist[1] = 0,其余节点的dist为正无穷大
2.找出一个未被标记的,dist最小的节点x,然后标记节点x
3.扫描节点所有的出边(x,y,z),若dist[y] > dist + z,则用后者更新dist[y]
O^2做法
int a[3010][3010],d[3010],n,m;
bool v[3010];
void dijkstra(){
memset(d,0x3f,sizeof(d));
memset(v,0,sizeof(v));
d[1] = 0;
for(int i = 1;i < n;i++){
int x = 0;
for(int j = 1;j <= n;j++){
if(!v[j] && (x == 0 || d[j] < d[x])) x = j;
v[x] = 1;//已经走过了
for(int y = 1;y <= n;y++){
d[y] = min(d[y],d[x] + a[x][y]);
}
}
}
}
int main(){
cin >> n >> m;
memset(a,0x3f,sizeof(a));
for(int i = 1;i <= n;i++) a[i][i] = 0;
for(int i = 1;i <= m;i++){
int x,y,z;
cin >> x >> y >> z;
a[x][y] = min(a[x][y],z);
}
dijkstra();
for(int i = 1;i <= n;i++){
cout << d[i];
}
}二叉堆优化(mlogn)
bool v[N];
int d[N];
int n,m,tot,s;
struct S{
int to,nxt,val;
}e[N];
void add1(int u,int v,int z){
e[++cnt].to = v;
e[cnt].nxt = head[u];
e[cnt].val = z;
head[u] = cnt;
}
std::priority_queue<std::pair<int,int>>q;
void dijkstra(){
memset(d,0x3f,sizeof(d));
memset(v,0,sizeof(v));
d[s] = 0; //s为原点
q.push(std::make_pair(0,s));
while(q.size()){
int x = q.top().second;q.pop();
if(v[x]) continue;
v[x] = 1;
for(int i = head[x];i;i = e[i].nxt){
int y = e[i].to,z = e[i].val;
if(d[y] > d[x] + z){
d[y] = d[x] + z;
q.push(std::make_pair(-d[y], y));
}
}
}
}
int main(){
cin >> n >> m;
for(int i = 1;i <= m;i++){
int x,y,z;
cin >> x >> y >> z;
add(x,y,z);
}
dijkstra();
for(int i = 1;i <= n;i++){
cout << d[i] << '\n';
}
}- 给定一张图,对于图中的某一条边(x,y,z),有dist[y] <= dist
- z成立,称该边满足三角形不等式。若所有边都满足三角形不等式,则dist数组就是所求最短路。
- 基于迭代方法的Bellman-Ford算法:
1.建立一个队列一开始只有起点1
2.取出队头节点x,扫描他的所有出边(x,y,z),若dist[y]>dist + z则用dist + z 来更新dist[y]
SPFA(Bellman-Ford算法优化)
const int N = 10010,M = 10010;
int head[N],ver[M],edge[M],next[M],d[N];
int n,m,tot;
queue<int>q;
bool v[N];
void add1(int u,int v,int z){
e[++cnt].to = v;
e[cnt].nxt = head[u];
e[cnt].val = z;
head[u] = cnt;
}
void spfa(){
memset(d,0x3f,sizeof(d));
memset(v,0,sizeof(v));
d[1] = 0;v[1] = 1;
q.push(1);
while(q.size()){
int x = q.front();
q.pop();
v[x] = 0;
for(int i = head[x];i;i = e[i].nxt){
int y = e[i].to,z = e[i].val;
if(d[y] > d[x] + z){
d[y] = d[x] + z;
if(!v[y]) q.push(y),v[y] = 1;
}
}
}
}
int main(){
cin >> n >> m;
for(int i = 1;i <= m;i++){
int x,y,z;
cin >> x >> y >> z;
add(x,y,z);
}
spfa();
for(int i = 1;i <= n;i++){
cout << d[i];
}
}(最近公共祖先)LCA
求两个点的最近公共祖先
#include <bits/stdc++.h>
using namespace std;
struct edge {
int to, nxt, val;
} e[100000001];
int head[100001], cnt;
void add(int from, int to) {
e[++cnt].to = to;
e[cnt].nxt = head[from];
head[from] = cnt;
}
int depth[500001], fa[500001][22], lg[500001];
void dfs(int now, int fath) {
fa[now][0] = fath;
depth[now] = depth[fath] + 1;
for (int i = 1; i <= lg[depth[now]]; i++) {
fa[now][i] = fa[fa[now][i - 1]][i - 1];
}
for (int i = head[now]; i; i = e[i].nxt) {
if (e[i].to != fath) dfs(e[i].to, now);
}
}
int LCA(int x, int y) {
if (depth[x] < depth[y]) swap(x, y);
while (depth[x] > depth[y]) {
x = fa[x][lg[depth[x] - depth[y]] - 1];
}
if (x == y) return x;
for (int k = lg[depth[x]] - 1; k >= 0; k--)
if (fa[x][k] != fa[y][k]) x = fa[x][k], y = fa[y][k];
return fa[x][0];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int n, m, s;
cin >> n >> m >> s; //s指的是
for (int i = 1; i <= n - 1; i++) {
int x, y;
cin >> x >> y;
add(x, y);
add(y, x);
}
for (int i = 1; i <= n; ++i)
lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
dfs(s, 0);
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
cout << LCA(x, y) << '\n' << flush;
}
system("pause");
return 0;
}最小生成树
Prim算法
int head[maxn],dis[maxn],cnt,n,m,tot,now=1,ans;
int prim(){
//先把dis数组附为极大值
for(int i=2;i<=n;++i){
dis[i]=inf;
}
//这里要注意重边,所以要用到min
for(int i=head[1];i;i=e[i].next){
dis[e[i].to]=std::min(dis[e[i].to],e[i].val);
}
while(++tot<n){
int minn=inf;
vis[now]=1;
for(int i=1;i<=n;++i){
if(!vis[i]&&minn>dis[i]){
minn=dis[i];
now=i;
}
}
ans+=minn;
//枚举now的所有连边,更新dis数组
for(int i=head[now];i;i=e[i].next){
int v=e[i].to;
if(dis[v]>e[i].val&&!vis[v]){
dis[v]=e[i].val;
}
}
}
return ans;
}Kruscal算法
#include<bits/stdc++.h>
using namespace std;
int read()
{
re int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*f;
}
struct Edge{
int u,v,w;
}edge[200005];
int fa[5005],n,m,ans,eu,ev,cnt;
bool cmp(Edge a,Edge b)
{
return a.w<b.w;
}
//快排的依据(按边权排序)
int find(int x)
{
while(x!=fa[x]) x=fa[x]=fa[fa[x]];
return x;
}
//并查集循环实现模板,及路径压缩,不懂并查集的同学可以戳一戳代码上方的“并查集详解”
void kruskal(){
sort(edge,edge+m,cmp);
//将边的权值排序
for(re int i=0;i<m;i++){
eu=find(edge[i].u), ev=find(edge[i].v);
if(eu==ev) continue;
//若出现两个点已经联通了,则说明这一条边不需要了
ans+=edge[i].w;
//将此边权计入答案
fa[ev]=eu;
//将eu、ev合并
if(++cnt==n-1) break;
//循环结束条件,及边数为点数减一时
}
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++){
fa[i]=i;
}
//初始化并查集
for(int i=0;i<m;i++)
{
edge[i].u=read(),edge[i].v=read(),edge[i].w=read();
}
kruskal();
cout <
return 0;
}匈牙利算法
(目的是尽可能更多的匹配)
把二分图分为A,B两个集合,依次枚举A中的每个点,试图在B集合中找到一个匹配。对于A集合中一个点x,假设B集合中有一个与其相连的点y,若y暂时还没有匹配点,那么x可以与y匹配:找到;
如果y已经有匹配点了,则回溯y匹配的点z,尝试着为z找一个除了y之外的匹配点,如果找到了,x和y可以匹配,否则两者无法匹配。
int M, N; //M, N分别表示左、右侧集合的元素数量
int Map[MAXM][MAXN]; //邻接矩阵存图
int p[MAXN]; //记录当前右侧元素所对应的左侧元素
bool vis[MAXN]; //记录右侧元素是否已被访问过
bool match(int i)
{
for (int j = 1; j <= N; ++j)
if (Map[i][j] && !vis[j]) //有边且未访问
{
vis[j] = true; //记录状态为访问过
if (p[j] == 0 || match(p[j])) //如果暂无匹配,或者原来匹配的左侧元素可以找到新的匹配
{
p[j] = i; //当前左侧元素成为当前右侧元素的新匹配
return true; //返回匹配成功
}
}
return false; //循环结束,仍未找到匹配,返回匹配失败
}
int Hungarian()
{
int cnt = 0;
for (int i = 1; i <= M; ++i)
{
memset(vis, 0, sizeof(vis)); //重置vis数组
if (match(i))
cnt++;
}
return cnt;
}最小点覆盖
想找到最少的点的数量,使得二分图的所有边都有一个端点在这些点中(就是删除掉这么多数量的点能够让所有的边能消失)
根据König定理可以得知,一个二分图中的最大匹配数等于这个图中的最小点覆盖数。于是得解。
Tarjan算法
求割点
割点的性质:
1.如果T的根节点是一个割点,当且仅当根节点有两个或者更多的子节点
2.T的非根节点cur是割点,当且仅当cur存在一个子节点nxt,nxt和他的后代都没有回退边连向cur的祖先
#include<bits/stdc++.h>
using std::cin,std::cout,std::deque,std::pair,std::queue,std::vector;
using LL = long long;
#define inf 0x3f3f3f3f
int qpow(int a, int n,int mod = 1e9 + 7){
int ans = 1; while(n){if(n & 1){ans = a * ans%mod;}a = a * a%mod;n >>= 1;}return ans%mod;
}
const int N = 2e5 + 10;
int head[N << 1],cnt;
struct edge{
int to,nxt,val;
}e[N<<1];
bool isCut[N];
void add(int u,int v){
e[++cnt].to = v;
e[cnt].nxt = head[u];
head[u] = cnt;
}
int low[N],dfn[N];
int tot = 0;
void tarjan(int now,int root){
low[now] = dfn[now] = ++tot;
int child = 0;
for(int i = head[now];i;i = e[i].nxt){
int to = e[i].to;
if(!dfn[to]){
child++;
tarjan(to,root);
low[now] = std::min(low[now],low[to]);
if(low[to] >= dfn[now] and now != root){
isCut[now] = true;
}
}
low[now] = std::min(low[now],dfn[to]);
}
if(child >= 2 && now == root){
isCut[root] = true;
}
}
void solve(){
int n,m;
cin >> n >> m;
for(int i = 1;i <= m;i++){
int u,v;
cin >> u >> v;
add(u,v);
add(v,u);
}
for(int root = 1;root <= n;root++){
if(!dfn[root]) tarjan(root,root);
}
vector<int> ans;
for(int i = 1;i <= n;i++){
if(isCut[i]) ans.push_back(i);
}
cout << ans.size() << '\n';
for(int i:ans){
cout << i << ' ';
}
cout << '\n';
}
signed main(){
std::ios::sync_with_stdio(false);
cin.tie(0);
int T;
T = 1;
// cin >> T;
while(T--){
solve();
}
}点双连通分量(vDcc)
点双连通分量:一个图中,点双连通的极大子图为一个点双连通分量。
性质:我们使用dfs找到一个割点之后,实际上已经完成了一个对于一个点双连通分量的访问。
使用一个栈来保存dfs的顺序。
和割点有关系
边双连通分量(eDCC)
性质:low值相同的点,必定在一个边双里。
强连通图缩点
强连通图指的是一张有向图内每个点一点都能到达任意的一个点
如果任意两点间存在路径,此称此图具有连通性,如下的图结构具有连通性。提及连通性,就不得不说连通分量,通俗而言,指结构中有多少个连通通道,如下的图结构只有一个连通通道,也就是一个连通分量,所有节点在这个连通通道上都能互通。
强连通是有向图的特定概念。有向图中,任意两点之间都可以连通,则认定此有向图为强连通图
若dfn[u] == low[u]这说明了𝑢点及𝑢点之下的所有子节点没有边是指向u的祖先的了,即我们之前说的𝑢点与它的子孙节点构成了一个最大的强连通图即强连通分量.
//tarjan
struct edge
{
int to,nxt,from,val;
}e[maxn*10],ed[maxn*10];
void add(int x,int y)
{
e[++cnt].from = x;
e[cnt].to = y;
head[x] = cnt;
}
int dfn[N], low[N], dfncnt, s[N], in_stack[N], tp;
int scc[N], sc; // 结点 i 所在 SCC 的编号
int sz[N]; // 强连通 i 的大小
void tarjan(int u) {
low[u] = dfn[u] = ++dfncnt, s[++tp] = u, in_stack[u] = 1;
for (int i = head[u]; i; i = e[i].nxt) {
const int &v = e[i].to;
if (!dfn[v]) {
tarjan(v);
low[u] = std::min(low[u], low[v]);
} else if (in_stack[v]) {
low[u] = std::min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
++sc;
while (s[tp] != u) {
scc[s[tp]] = sc;
sz[sc]++;
in_stack[s[tp]] = 0;
--tp;
}
scc[s[tp]] = sc;
sz[sc]++;
in_stack[s[tp]] = 0;
--tp;
}
}
int main(){
int n;
cin >> n;
for(int i=1;i<=n;i++)
if(!dfn[i])tarjan(i);
for(int i=1;i<=n;i++)
{
for(int j=head[i];j;j=e[j].nxt)
{
int xx=e[j].to;// 原边,若不是一个强联通分量的,再在现图上加边
if(color[i]!=color[xx])
add_edge(color[i],color[xx]);// 加边
}
}
return 0;
}网络最大流
拥有源点还有一个汇点,其上的边权称为容量,网络流中常见的问题就是网络最大流,假定从源点流出的流量足够多,求能够流入汇点的最大流量
解决这个问题最常用的是Ford-Fulkerson算法及其优化。
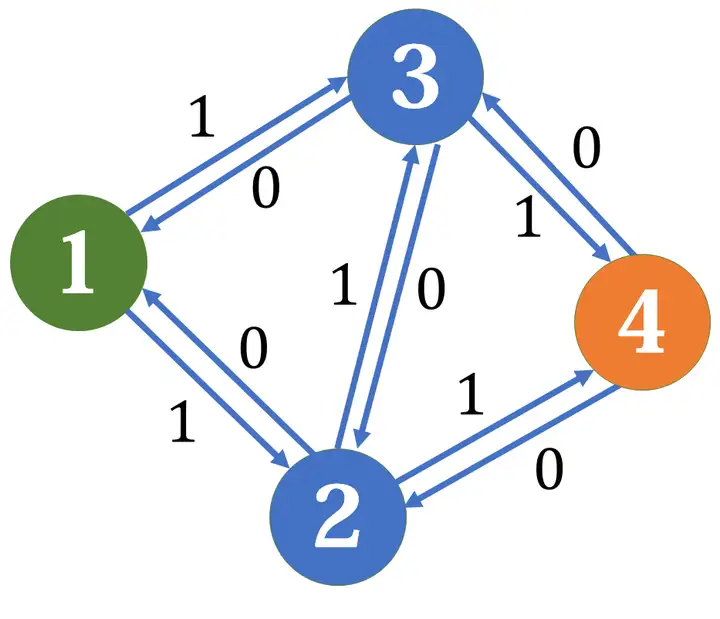
img
FF算法通过增广路和反向边(相当于一种反悔机制)
Ford-Fulkerson
int n, m, s, t; // s是源点,t是汇点
bool vis[MAXN];
int dfs(int p = s, int flow = INF)
{
if (p == t)
return flow; // 到达终点,返回这条增广路的流量
vis[p] = true;
for (int eg = head[p]; eg; eg = edges[eg].next)
{
int to = edges[eg].to, vol = edges[eg].w, c;
// 返回的条件是残余容量大于0、未访问过该点且接下来可以达到终点(递归地实现)
// 传递下去的流量是边的容量与当前流量中的较小值
if (vol > 0 && !vis[to] && (c = dfs(to, min(vol, flow))) != -1)
{
edges[eg].w -= c;
edges[eg ^ 1].w += c;
// 这是链式前向星取反向边的一种简易的方法
// 建图时要把cnt置为1,且要保证反向边紧接着正向边建立
return c;
}
}
return -1; // 无法到达终点
}
inline int FF()
{
int ans = 0, c;
while ((c = dfs()) != -1)
{
memset(vis, 0, sizeof(vis));
ans += c;
}
return ans;
}Edmond-Karp
int n, m, s, t, last[MAXN], flow[MAXN];
inline int bfs()
{
memset(last, -1, sizeof(last));
queue<int> q;
q.push(s);
flow[s] = INF;
while (!q.empty())
{
int p = q.front();
q.pop();
if (p == t) // 到达汇点,结束搜索
break;
for (int eg = head[p]; eg; eg = edges[eg].next)
{
int to = edges[eg].to, vol = edges[eg].w;
if (vol > 0 && last[to] == -1) // 如果残余容量大于0且未访问过(所以last保持在-1)
{
last[to] = eg;
flow[to] = min(flow[p], vol);
q.push(to);
}
}
}
return last[t] != -1;
}
inline int EK()
{
int maxflow = 0;
while (bfs())
{
maxflow += flow[t];
for (int i = t; i != s; i = edges[last[i] ^ 1].to) // 从汇点原路返回更新残余容量
{
edges[last[i]].w -= flow[t];
edges[last[i] ^ 1].w += flow[t];
}
}
return maxflow;
}Dinic算法
#include <bits/stdc++.h>
#define ll long long
using namespace std;
#define INF INT_MAX
const int N = 820010;
int head[N],cnt = 1;
struct node{
ll next,w,to;
}edges[N<<1];
void add(int u,int v,int val){
edges[++cnt].to = v;
edges[cnt].w = val;
edges[cnt].next = head[u];
head[u] = cnt;
}
int n, m, s, t, lv[N], cur[N]; // lv是每个点的层数,cur用于当前弧优化标记增广起点
inline bool bfs() // BFS分层
{
memset(lv, -1, sizeof(lv));
lv[s] = 0;
memcpy(cur, head, sizeof(head)); // 当前弧优化初始化
queue<int> q;
q.push(s);
while (!q.empty())
{
int p = q.front();
q.pop();
for (int eg = head[p]; eg; eg = edges[eg].next)
{
int to = edges[eg].to, vol = edges[eg].w;
if (vol > 0 && lv[to] == -1)
lv[to] = lv[p] + 1, q.push(to);
}
}
return lv[t] != -1; // 如果汇点未访问过说明已经无法达到汇点,此时返回false
}
int dfs(int p = s, int flow = INF)
{
if (p == t)
return flow;
int rmn = flow; // 剩余的流量
for (int eg = cur[p]; eg && rmn; eg = edges[eg].next) // 如果已经没有剩余流量则退出
{
cur[p] = eg; // 当前弧优化,更新当前弧
int to = edges[eg].to, vol = edges[eg].w;
if (vol > 0 && lv[to] == lv[p] + 1) // 往层数高的方向增广
{
int c = dfs(to, min(vol, rmn)); // 尽可能多地传递流量
rmn -= c; // 剩余流量减少
edges[eg].w -= c; // 更新残余容量
edges[eg ^ 1].w += c; // 再次提醒,链式前向星的cnt需要初始化为1(或-1)才能这样求反向边
}
}
return flow - rmn; // 返回传递出去的流量的大小
}
inline int dinic()
{
int ans = 0;
while (bfs())
ans += dfs();
return ans;
}
void solve(){
cin >> n >> m >> s >> t;
for(int i = 1;i <= m;i++){
int u,v,val;
cin >> u >> v >> val;
add(u,v,val);
add(v,u,0);
}
int ans = dinic();
cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0);
int T = 1;
//cin >> T;
while(T--){
solve();
}
}最小割
一个网络的割是这样一个边集,如果把这个集合的边删去,这个网络就不再连通,这个边集中边的容量和被称为割的容量,容量最小的割被称为最小割
最大流最小割定理
对于一个容量网络,其最大流等于最小割的容量
路径覆盖问题
路径覆盖问题是在DAG(有向无环图)上进行的,找出尽可能少的一系列路径,使得这些路径经过DAG上所有的点恰好一次。可以用网络流来解决这个问题,
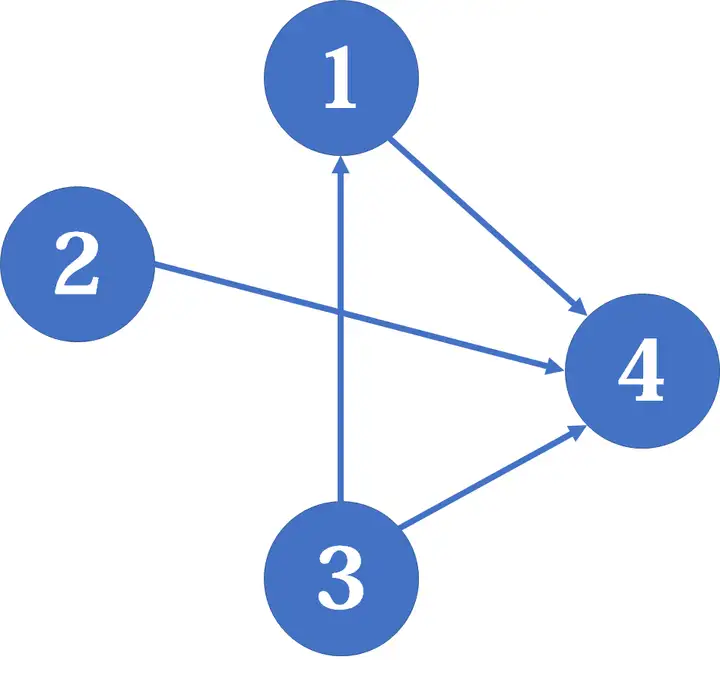
img
以这张图片为例,建立网络流模型,把原图中的每个点拆成两个点,其中一个点与源点相连,另一个点与汇点相连。(对于点x,可以把从它拆出去的点记为x+n)
计算几何
二维几何基础
| 计算几何基础函数 |
| 1.点和向量的定义 |
| 2.向量的基本运算 |
| 3.点积 |
| 4.向量长度 |
| 5.两向量角度 |
| 6.叉积(2向量/3点) |
| 7.向量旋转 |
| 8.向量的单位法线 |
| 9.求两点距离 |
| 10.直线(射线)交点 |
| 11.点到直线的距离 |
| 12.点到线段的距离 |
| 13.点在直线上的投影 |
| 14.线段相交判定(规范相交)|
| 15.点是否在一条线段上 |
| 16.求多边形面积 |
| 17.判断点是否在多边形内 |
| 18.求凸包 |
| 19.求凸包周长 |
| 20.求多边形面积 |
#include <iostream>
#include <cmath>
using namespace std;
#define eps 1e-10
/********** 定义点 **********/
struct Point{
double x,y;
Point(double x=0,double y=0):x(x),y(y) {}
};
/********** 定义向量 **********/
typedef Point Vector;
/********** 向量 + 向量 = 向量 **********/
Vector operator + (Vector a,Vector b)
{
return Vector(a.x+b.x,a.y+b.y);
}
/********** 点 - 点 = 向量 **********/
Vector operator - (Point a,Point b)
{
return Vector(a.x-b.x,a.y-b.y);
}
/********** 向量 * 数 = 向量 **********/
Vector operator * (Vector a,double b)
{
return Vector(a.x*b,a.y*b);
}
/********** 向量 / 数 = 向量 **********/
Vector operator / (Vector a,double b)
{
return Vector(a.x/b,a.y/b);
}
bool operator < (const Point& a,const Point& b)
{
return a.x<b.x || (a.x==b.x && a.y<b.y);
}
int dcmp(double x) //减少精度问题
{
if(fabs(x)<eps)
return 0;
else
return x<0?-1:1;
}
bool operator == (const Point &a,const Point &b) //判断两点是否相等
{
return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
}
/********** 向量点积 **********/
double Dot(Vector a,Vector b)
{
return a.x*b.x+a.y*b.y;
}
/********** 向量长度 **********/
double Length(Vector A)
{
return sqrt(Dot(A,A));
}
/********** 两向量角度 *********/
double Angle(Vector A,Vector B)
{
return acos(Dot(A,B)/Length(A)/Length(B));
}
/********** 2向量求叉积 **********/
double Cross(Vector a,Vector b)
{
return a.x*b.y-b.x*a.y;
}
/********** 3点求叉积 **********/
double Cross(Point a,Point b,Point c)
{
return (c.x-a.x)*(b.y-a.y) - (c.y-a.y)*(b.x-a.x);
}
/********** 向量旋转 ***********/
Vector Rotate(Vector A,double rad)
{
return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
/********** 向量的单位法线 *********/
Vector Normal(Vector A)
{
double L = Length(A);
return Vector(-A.y/L,A.x/L);
}
/********** 点和直线 **********/
/********** 求两点间距离 **********/
double dist(Point a,Point b)
{
return sqrt( (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y) );
}
/********** 直线交点 **********/
Point GetLineIntersection(Point P,Vector v,Point Q,Vector w)
{
Vector u = P-Q;
double t = Cross(w,u) / Cross(v,w);
return P+v*t;
}
/********** 点到直线的距离 ***********/
double DistanceToLine(Point P,Point A,Point B)
{
Vector v1 = B-A,v2 = P-A;
return fabs(Cross(v1,v2)) / Length(v1); //如果不取绝对值,得到的是有向距离
}
/********** 点到线段的距离 **********/
double DistanceToSegment(Point P,Point A,Point B)
{
if(A==B) return Length(P-A);
Vector v1 = B-A,v2 = P-A,v3 = P-B;
if(dcmp(Dot(v1,v2))<0) return Length(v2);
else if(dcmp(Dot(v1,v3)) > 0) return Length(v3);
else return fabs(Cross(v1,v2)) / Length(v1);
}
/********** 点在直线上的投影 ***********/
Point GetLineProjection(Point P,Point A,Point B)
{
Vector v = B-A;
return A+v*(Dot(v,P-A) / Dot(v,v));
}
/********** 线段相交判定(规范相交) ************/
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)
{
double c1 = Cross(a2-a1,b1-a1),c2 = Cross(a2-a1,b2-a1),
c3 = Cross(b2-b1,a1-b1),c4 = Cross(b2-b1,a2-b1);
return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}
/********* 点是否在一条线段上 **********/
bool OnSegment(Point p,Point a1,Point a2)
{
return dcmp(Cross(a1-p,a2-p)) == 0 && dcmp(Dot(a1-p,a2-p)) <0 ;
}
/********* 求多边形面积 **********/
double ConvexPolygonArea(Point* p,int n)
{
double area = 0;
for(int i=1;i<n-1;i++)
area += Cross(p[i]-p[0],p[i+1]-p[0]);
return area/2;
}
/********** 判断点是否在多边形内 **********/
//判断点q是否在多边形内
//任意凸或者凹多边形
//顶点集合p[]按逆时针或者顺时针顺序存储(1..pointnum)
struct Point{
double x,y;
};
struct Line{
Point p1,p2;
};
double xmulti(Point p1,Point p2,Point p0) //求p1p0和p2p0的叉积,如果大于0,则p1在p2的顺时针方向
{
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
double Max(double a,double b)
{
return a>b?a:b;
}
double Min(double a,double b)
{
return a<b?a:b;
}
bool ponls(Point q,Line l) //判断点q是否在线段l上
{
if(q.x > Max(l.p1.x,l.p2.x) || q.x < Min(l.p1.x,l.p2.x)
|| q.y > Max(l.p1.y,l.p2.y) || q.y < Min(l.p1.y,l.p2.y) )
return false;
if(xmulti(l.p1,l.p2,q)==0) //点q不在l的延长线或者反向延长线上,如果叉积再为0,则确定点q在线段l上
return true;
else
return false;
}
bool pinplg(int pointnum,Point p[],Point q)
{
Line s;
int c = 0;
for(int i=1;i<=pointnum;i++){ //多边形的每条边s
if(i==pointnum)
s.p1 = p[pointnum],s.p2 = p[1];
else
s.p1 = p[i],s.p2 = p[i+1];
if(ponls(q,s)) //点q在边s上
return true;
if(s.p1.y != s.p2.y){ //s不是水平的
Point t;
t.x = q.x - 1,t.y = q.y;
if( (s.p1.y == q.y && s.p1.x <=q.x) || (s.p2.y == q.y && s.p2.x <= q.x) ){ //s的一个端点在L上
int tt;
if(s.p1.y == q.y)
tt = 1;
else if(s.p2.y == q.y)
tt = 2;
int maxx;
if(s.p1.y > s.p2.y)
maxx = 1;
else
maxx = 2;
if(tt == maxx) //如果这个端点的纵坐标较大的那个端点
c++;
}
else if(xmulti(s.p1,t,q)*xmulti(s.p2,t,q) <= 0){ //L和边s相交
Point lowp,higp;
if(s.p1.y > s.p2.y)
lowp.x = s.p2.x,lowp.y = s.p2.y,higp.x = s.p1.x,higp.y = s.p1.y;
else
lowp.x = s.p1.x,lowp.y = s.p1.y,higp.x = s.p2.x,higp.y = s.p2.y;
if(xmulti(q,higp,lowp)>=0)
c++;
}
}
}
if(c%2==0)
return false;
else
return true;
}
/********** 求凸包 **********/
struct Point{
double x,y;
};
double dis(Point p1,Point p2)
{
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
double xmulti(Point p1,Point p2,Point p0) //求p1p0和p2p0的叉积,如果大于0,则p1在p2的顺时针方向
{
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
int graham(Point p[],int n,int pl[]) //点集,点的个数,凸包顶点集
{
int pl[10005];
//找到纵坐标(y)最小的那个点,作第一个点
int t = 1;
for(int i=1;i<=n;i++)
if(p[i].y < p[t].y)
t = i;
pl[1] = t;
//顺时针找到凸包点的顺序,记录在 int pl[]
int num = 1; //凸包点的数量
do{ //已确定凸包上num个点
num++; //该确定第 num+1 个点了
t = pl[num-1]+1;
if(t>n) t = 1;
for(int i=1;i<=n;i++){ //核心代码。根据叉积确定凸包下一个点。
double x = xmulti(p[i],p[t],p[pl[num-1]]);
if(x<0) t = i;
}
pl[num] = t;
} while(pl[num]!=pl[1]);
return num-1; //凸包顶点数
}
/********** 求凸包周长 **********/
struct Point{
double x,y;
};
double dis(Point p1,Point p2)
{
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
double xmulti(Point p1,Point p2,Point p0) //求p1p0和p2p0的叉积,如果大于0,则p1在p2的顺时针方向
{
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
double graham(Point p[],int n) //点集和点的个数
{
int pl[10005];
//找到纵坐标(y)最小的那个点,作第一个点
int t = 1;
for(int i=1;i<=n;i++)
if(p[i].y < p[t].y)
t = i;
pl[1] = t;
//顺时针找到凸包点的顺序,记录在 int pl[]
int num = 1; //凸包点的数量
do{ //已确定凸包上num个点
num++; //该确定第 num+1 个点了
t = pl[num-1]+1;
if(t>n) t = 1;
for(int i=1;i<=n;i++){ //核心代码。根据叉积确定凸包下一个点。
double x = xmulti(p[i],p[t],p[pl[num-1]]);
if(x<0) t = i;
}
pl[num] = t;
} while(pl[num]!=pl[1]);
//计算凸包周长
double sum = 0;
for(int i=1;i<num;i++)
sum += dis(p[pl[i]],p[pl[i+1]]);
return sum;
}
/********** 求多边形面积 **********/
struct Point{ //定义点结构
double x,y;
};
double getS(Point a,Point b,Point c) //返回三角形面积
{
return ((b.x - a.x) * (c.y - a.y) - (b.y - a.y)*(c.x - a.x))/2;
}
double getPS(Point p[],int n) //返回多边形面积。必须确保 n>=3,且多边形是凸多边形
{
double sumS=0;
for(int i=1;i<=n-1;i++)
sumS+=getS(p[1],p[i],p[i+1]);
return sumS;
}旋转卡壳(求凸包的直径)
这里模板求的是直径的平方
const double eps=1e-9;
int dcmp(double x){
return (fabs(x)<=eps)?0:(x<0?-1:1);
}
struct Point{
double x,y;
Point(double X=0,double Y=0){x=X,y=Y;}
};
struct Vector{
double x,y;
Vector(double X=0,double Y=0){x=X,y=Y;}
};
inline Vector operator-(Point x,Point y){// 点-点=向量
return Vector(x.x-y.x,x.y-y.y);
}
inline double cross(Vector x,Vector y){ // 向量叉积
return x.x*y.y-x.y*y.x;
}
inline double operator*(Vector x,Vector y){ // 向量叉积
return cross(x,y);
}
inline double len(Vector x){ // 向量模长
return sqrt(x.x*x.x+x.y*x.y);
}
int stk[50005];
bool used[50005];
vector<Point> ConvexHull(Point* poly, int n){ // Andrew算法求凸包
int top=0;
sort(poly+1,poly+n+1,[&](Point x,Point y){
return (x.x==y.x)?(x.y<y.y):(x.x<y.x);
});
stk[++top]=1;
for(int i=2;i<=n;i++){
while(top>1&&dcmp((poly[stk[top]]-poly[stk[top-1]])*(poly[i]-poly[stk[top]]))<=0){
used[stk[top--]]=0;
}
used[i]=1;
stk[++top]=i;
}
int tmp=top;
for(int i=n-1;i;i--){
if(used[i]) continue;
while(top>tmp&&dcmp((poly[stk[top]]-poly[stk[top-1]])*(poly[i]-poly[stk[top]]))<=0){
used[stk[top--]]=0;
}
used[i]=1;
stk[++top]=i;
}
vector<Point> a;
for(int i=1;i<=top;i++){
a.push_back(poly[stk[i]]);
}
return a;
}
struct Line{
Point x;Vector y;
Line(Point X,Vector Y){x=X,y=Y;}
Line(Point X,Point Y){x=X,y=Y-X;}
};
inline double DistanceToLine(Point P,Line x){// 点到直线的距离
Vector v1=x.y, v2=P-x.x;
return fabs(cross(v1,v2))/len(v1);
}
double RoatingCalipers(vector<Point> poly){// 旋转卡壳
if(poly.size()==3) return len(poly[1]-poly[0]);
int cur=0;
double ans=0;
for(int i=0;i<poly.size()-1;i++){
Line line(poly[i],poly[i+1]);
while(DistanceToLine(poly[cur], line) <= DistanceToLine(poly[(cur+1)%poly.size()], line)){
cur=(cur+1)%poly.size();
}
ans=max(ans, max(len(poly[i]-poly[cur]), len(poly[i+1]-poly[cur])));
}
return ans;
}
Point poly[50005];
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>poly[i].x>>poly[i].y;
double v=RoatingCalipers(ConvexHull(poly, n));
cout<<(int)(v*v);
return 0;
}圆和球
#include <iostream>
#include <cmath>
using namespace std;
#define eps 1e-10
/********** 定义点 **********/
struct Point{
double x,y;
Point(double x=0,double y=0):x(x),y(y) {}
};
/********** 定义三维点 ***********/
struct Point3{
double x,y,z;
Point3(double x=0,double y=0,double z=0):x(x),y(y),z(z) {}
};
/********** 定义圆 **********/
struct Circle{
Point c;
double r;
Circle(Point c,double r):c(c),r(r){}
Point point(double a){
return Point(c.x + cos(a)*r,c.y + sin(a)*r);
}
};
/*********** 三维点距离 **********/
double dis3(Point3 A,Point3 B)
{
return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y)+(A.z-B.z)*(A.z-B.z));
}
/*********** 球面 ***********/
/*********** 角度转换成弧度 ***********/
double torad(double deg)
{
return deg/180 * acos(-1); //acos(-1)就是PI
}
/*********** 经纬度(角度)转化为空间坐标 **********/
void get_coord(double R,double lat,double lng,double &x ,double &y,double &z)
{
lat = torad(lat); //纬度
lng = torad(lng); //经度
x = R*cos(lat)*cos(lng);
y = R*cos(lat)*sin(lng);
z = R*sin(lat);
}
/*********** 两点的球面距离 ***********/s
double disA2B(double R,Point3 A,Point3 B)
{
//将球面距离看成求点A,B和半径R构成的扇形的弧长
double d = dis3(A,B); //弦长
double a = 2*asin(d/2/R); //圆心角
double l = a*R; //弧长
return l;
}海伦公式形态的四面体体积公式
一般海伦公式:公式中a,b,c分别为三角形三边长,p为半周长,S为三角形的面积。
以下内容转自维基百科
如果U、V、W、u、v、w是四面体的六条边长(U、V、W构成四面体的其中一个三角形面,而u是与U相对的棱,v是与V相对的棱,w是与W相对的棱),则四面体体积

这里
